Logarithms Using the Graphing Calculator

logo

Working with Logarithms

A logarithm is an exponent.

As this example shows, 3 is the exponent to which the base 2 must be raised to create the answer of 8,
or 2³ = 8. In general terms:

(where x > 0 and b is a positive constant not equal to 1)

Entering logarithms on the graphing calculator.

Versions for both newer and older calculators

The log key will calculate common
(base 10) logarithms.

The ln key will calculate natural
(base e) logarithms.

To enter other log bases :
• Use logBASE( template at MATH → arrow down to A:logBASE(.

For older calculator models:
• Use the following "change of base" conversion formula:
logcalcformula
Example:
For log₂ x. enter log(x) / log(2)

Beware of Graphs:

		For TI-84+CE Don't confuse log graphs with square root graphs. At fist glance, these two graphs appear to be similar. But the square root graph is actually ending, while the log graph is not.
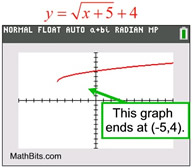	On the logarithmic graph above, the calculator is "trying" to plot points on the graph to the left. But the graph is SO CLOSE to the asymptote of x = -5, there is no room to put additional pixels before it crosses over the asymptote. Plotting points "straight" down would violate the graph being a function, and the TI-84+ plots functions.

Types of Logarithms:

BASE 10:

Logarithms with base 10 are called common logarithms.
When the base is not indicated, base 10 is implied.
The log key on the graphing calculator will calculate the
common (or base 10) logarithm.
2nd log will calculate the antilogarithm or 10^x
logpic1

OTHER BASES:

• If your calculator has the logBASE operation template, you can enter the values as they appear in the expression.
Go to: MATH → arrow down to A:logBASE(
and the template to enter values will appear.
Or hit MATH, ALPHA (key), MATH to get to the A: option.

• To enter a logarithm with a different base on an older model graphing calculator, use the Change of Base Formula:
log7

• You can also hit ALPHA (key), WINDOW
and choose the fifth option on the menu, logBASE(.

BASE e:

Logarithms with base e are called natural logarithms.
Natural logarithms are denoted by ln.
On the graphing calculator, the base e logarithm is the ln key.

e 2.71828183

All three are the same.

Note: If you are working with an older model of the TI-84+ calculator,
you may need to use (and remember) the "Change of Base Formula"
for entering logarithms:

Remember, the notation:
log x is with respect to base 10
ln x is with respect to base e

Examples:

1. Evaluate: log94

2. Evaluate: ln 2; ln 1; ln e

3. Evaluate:

4. Sketch the graph of l18

If you have the logBASE template function, it can be used to enter the function (seen at the right).
If not, use the Change of Base formula, as seen below.

5. Use a graph to support the conclusion that the inverse of l19

A function composed with its inverse creates the identity line y = x. Showing that the composition of these two functions is the identity line shows that these functions are inverses of one another. Note the bubble animation (-o) set for Y₄ to show that the linear lines in Y₃ and Y₄ are equivalent.
You are showing that the composition of Y1(Y2) = x (the Identity Function).

6. Solve graphically: l21

Method 1: Graph each side separately.
The window must be adjusted to show a sufficient amount of the x-axis to locate the intersection point (2nd CALC, #5). The answer is x = 32.

Method 2: This problem can also be solved by setting the equation equal to 0 and finding the x-intercepts, or zeros (2nd CALC, #2), of the function. Function: log₄x - 2.5 = 0

7. Using your graphing calculator, determine which of the following statements are true.
l27

a.) T b.) F c.) F d.) T e.) F f.) T

Solution for part a: (TRUE)
Place the left side of the equation in Y₁ and the right side in Y₂. Turn on the "bubble animation" to the left of the Y₂. This will allow you to see the bubble floating over the graph when the equation is true. Parts b - f are solved in a similar manner.

Finding Your Way Around TABLE of CONTENTS